

发布时间:2024-11-08 20:20
作者:admin
聪明如你,请做题:
一个盲人有5双白袜子和5双黑袜子,除了颜色差异,其它一模一样,弄混了,请问如何分开?
这是一个简单而有启示的智力题。
答案很简单:拿到太阳下去晒。
在阳光下,黑袜子吸热更快,所以通过触摸,盲人可以感知到袜子的温度差异,从而将白袜子和黑袜子分开。
最初,盲人只能通过触摸袜子的材质,但无法区分颜色。因此,我们可以引入“温度”这个维度,通过阳光加热,创造了一个新的识别维度(温度差)。
这就类似于在复杂问题中引入额外的信息维度,以便更好地理解问题。
我曾经写过“灰度认知,黑白决策”,本文像是下联。
顺着这一点,我想谈及信息的“维度”。
最有名的“升维思考”,也许是爱因斯坦的相对论。
在牛顿物理学中,我们处理的通常是三维空间中的物体运动,时间是一个独立的量。
但爱因斯坦在狭义相对论中提出了一个全新的框架,称为四维时空,将时间和空间视为相互关联的统一结构。
在广义相对论中,物质和能量会弯曲时空,而物体在弯曲时空中的运动实际上是沿着时空曲线运动。
由此,人类对物理世界有了更加精确的解释。
就你我而言,我们究竟是如何理解这个世界的?我们如何判断一个未知的事物?我们如何在信息不充分的情况下做出决策?
也许每个人都是如盲人摸像一般,通过不同角度的特征做出推断。
了不起的高手,往往比普通人有更高的认知维度,例如围棋天才独具的“感觉”,杨振宁推崇的“Taste”。
AI通过降维简化问题,通过升维来揭示更多的隐藏信息,这一点在深度学习的领域产生了神奇的效果,以至于机器可以获得8年前人类还自以为独具的“感觉”。
在大模型时代,AI借助于算法、算力和数据,获得了在某些方面超越人类的“高维思考”能力。
而此时,人类的联想和提问能力,就像是构建一个维度,或是在大模型的向量空间里,勾出一段彩虹。
就像扔出一个骰子,对于未来的可能性,我们要升维思考,考虑6个面的概率,可结果只有一面。
这大概是“升维思考、降维行动”的一个简单隐喻。
《人工智能:现代方法》说:
人工智能(artificial intelligence,AI)领域不仅涉及理解,还涉及构建智能实体。这些智能实体机器需要在各种各样新奇的情况下,计算如何有效和安全地行动。
我们需要理性思考,也需要理性行为,尤其要在“存在不确定性时取得最佳期望结果而采取行动。”
升维思考与灰度认知,都和概率论有关,再加上基于时间的与外部环境的互动,贝叶斯定律常常现身其中。
更现实一点的场景是:对于一个投资者,需要升维思考。例如芒格的多元思维模型。但是他的模型是通过多个维度的证伪,来切割出钻石的。--本文提及的朴素贝叶斯分类,底层的原理(可感知的那部分)是想通的。
而行动本身,往往是降维的。
从数学的角度看,我们需要一个(相对)最优概率;
从物理的角度看,系统需要(相对)最低势能状态;
从决策的角度看,人类必须采取行动并接受一个黑白分明的结果。
多面骰子在空中飞舞,最终只能选择一面朝上。
投资者最终需要做出“买或不买、卖或不买”的决策,而且行动越少越简单越好。
降维行动的例子:京东说要“多快好省”,拼多多只要一个“省”。
那些大事不糊涂的人,那些过得不错并且还能轻松的人,大多是在维度上取得了胜利。
现在做事不容易,许多行业和公司都在谈“转型”。但是,如果没有维度上的突破,可能只是在原路上瞎扑腾。
活在二维世界里的生物的死局,往往要靠超越维度来破解。
“井底之蛙”看似是关于视野的隐喻,其实是关于维度的类比。
本文从一个我喜欢的智力题开始,将毒酒问题的二进制解法,类比为更高维度的胜利。
类比可能是鲜活的,但绝不严谨。甚至于在文章的推进过程中,升维和降维都会出现一些概念的交错。
类比和隐喻都是思考的脚手架,请你能用且用,用完后记得拆除。
更广阔的意义上,每个人都是全体人类的一个维度。
所以,请活出你自己。
一
让我们从一道有趣的题开始:
国王有一百桶酒,比自己的生命还重要。结果有一天其中一桶被投了慢性毒药,喝了以后半个小时就会死掉。国王大怒,命令玩忽职守的侍卫去试毒。酒不能被混合,一个侍卫可以喝多桶酒,一桶酒也可以由多个侍卫喝。
请问:怎么样才能用最少的侍卫、在半小时内知道哪桶是毒酒?
最简单的方案,是让每个人试一桶酒,用时30分钟,就可以判断出哪一桶酒有毒。
这个是“一维”的直线思维,在现实生活中也未尝不可,好过什么都不干。
这样的解法,答案是:99个人。
从二维层面去思考,引入笛卡尔的坐标。
把100桶酒摆成10✖️10的矩阵,如下:
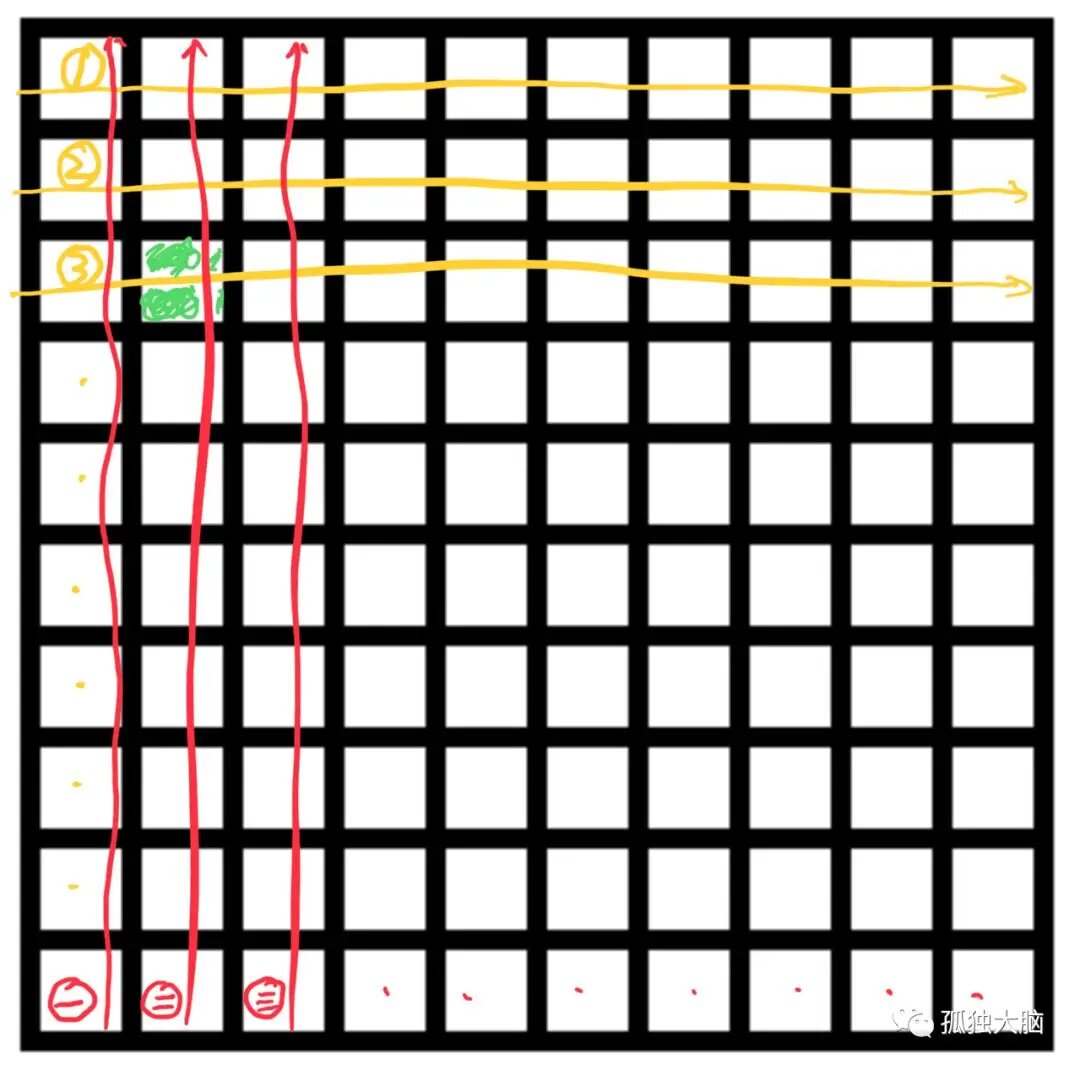
接下来:
1. 让阿拉伯数字编号的1号侍卫(如上图,黄色),把第1行酒每桶喝一口,一直到10号喝第10行;
2. 让汉字编号的一号侍卫,把第一列酒每桶喝一口,一直到十号喝第十列;
3. 由于坐标的定位功能,假如毒酒在图中绿色的位置,那么3号侍卫和二号侍卫都会死,自然可以锁定毒酒的位置。
4. 但是因为第10行和第十列可以不用安排人,也能获取信息,所以可以减少两个人。
这样的解法,答案是:18个人。
能否再延伸至三维层面去思考呢?
我们很容易想到,搭建一个5✖️5✖️4的三维模型,正好有100个位置放酒,如下:
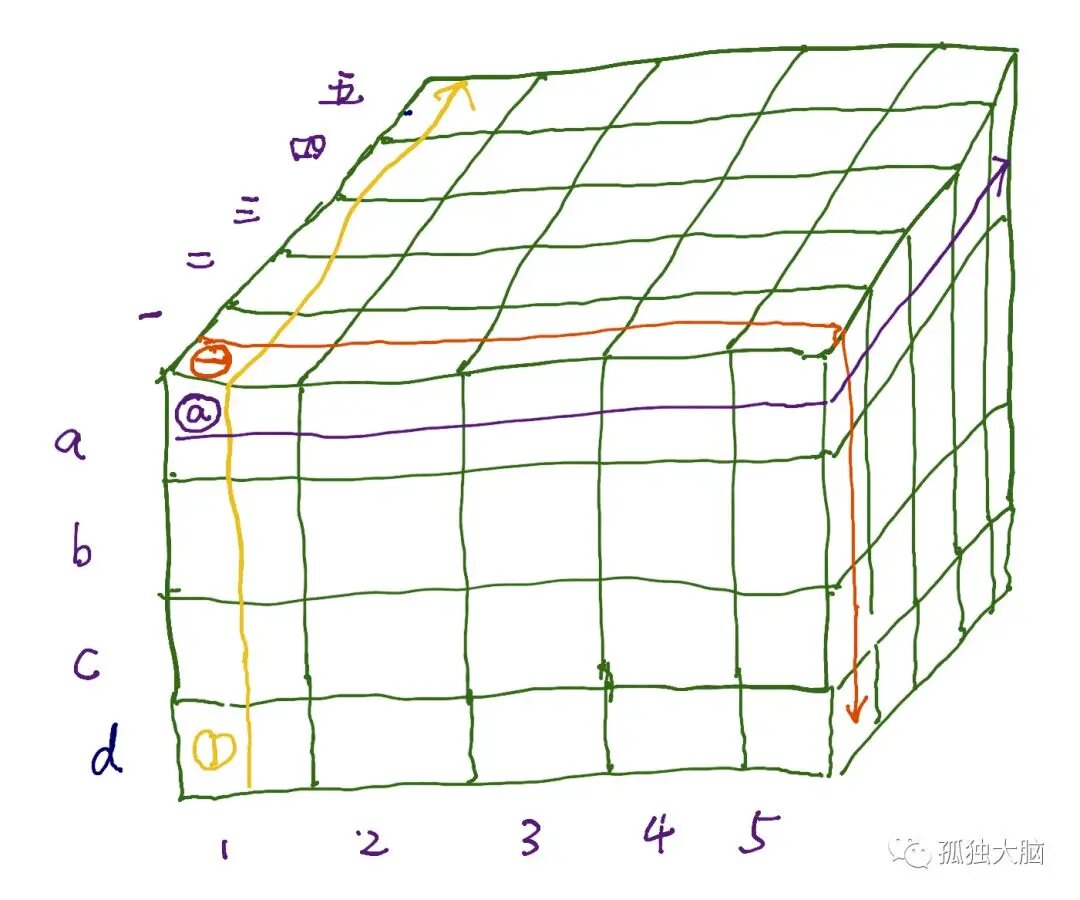
接下来(和二维解法差不多):
1. 让阿拉伯数字编号的1号侍卫(如上图,黄色),把黄色箭头这一面墙的酒每桶喝一口,一直到5号喝第5面墙;
2. 让汉字编号的一号侍卫(如上图,橙色),把橙色箭头这一面墙的酒每桶喝一口,一直到五号喝第五面墙;
3. 让字母编号的a号侍卫(如上图,蓝色),把蓝色箭头这一层的酒每桶喝一口,一直到d号喝第四层;
4. 同理,通过三个维度,也可以锁定毒酒的位置;
5. 以及,每个维度都可以少一个人。
这样的解法,答案是:11个人。
最笨的方法1,会死一个侍卫;方法2会死两个(或1个,或零个),方法3会死三个(或两个,或一个,或零个),总之一个维度需要获取一个信息,可能会死一个,或者提供零的信息。
所以题目中有含糊的地方,到底是用最少的侍卫,还是死最少的侍卫?考虑到国王的残酷,我们姑且认为是前者。
然而,即使聪明如你想明白了上面三个维度的解法,还是没有找到最优答案。
如果用计算机的思维来分析这个问题,那么首先考虑如何存储这100桶酒。100桶酒可以用二进制7个比特来表示(2的7次方>100)。
上面的解法1到解法3,都是用100个位置存储100桶酒,只是描述位置的坐标,从一维到三维,效率越来越高,所以用的侍卫越来越少。
如果用二进制呢?
二进制,是逢二进一的计数编码方法,只有0和1两个数码。那到了2怎么办?只有往前进一位,变成10。
所以,十进制的2、3、4、5,二进制分别表示为10、11、100、101。二进制广泛应用于电子计算机的数据处理。
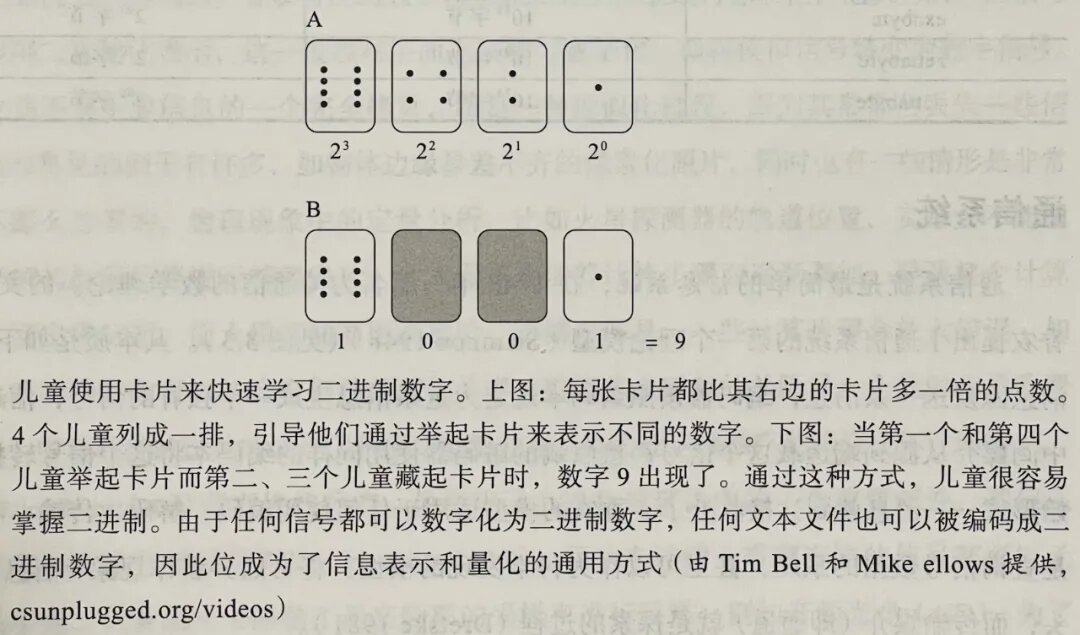
回到我们的题目,计算如下:
第一步:对于每一桶酒的二进制表示,编码后,最长的数字是7位数,不足七位前面用0表示;
1号桶是0000001,
2号桶是0000010,
3号桶是0000011,
4号桶是0000100,
……
100号桶是1100100;
第二步:可以找七个侍卫,从左到右,编号“一”至“七”,每人对应一个位数,从第一位到第七位。
第三步:负责第一位数的侍卫“一”,只要这100桶酒中,二进制编码的该位数对应的数字是1,则喝掉此桶酒。
如此类推,每个侍卫喝掉他所负责的位数上数字是1的酒。
第四步:30分钟后,侍卫按照“一”至“七”,死掉的置为1,活着的置为0。
例如,假如第七桶酒为毒酒,其二进制编码是0000111。那么按照上面的喝酒规则,其五、六、七位都是“1”,所以编号五、六、七的侍卫都会死。
前四个侍卫,遇到这瓶毒酒,因为对应的数字是0,所以都会活。
二进制的0和1,正好对应了活和死。
根据7个侍卫喝酒后半小时的生死状态,能够得出毒酒的二进制编码。
这样的解法,答案是:7个人。
以下,请允许我从一个非专业人士的“感知”的角度,来说说这道题的启示:
1、第一种方法,是简单的线性搜索;
2、第二、第三两种方法,是增加了维度的线性搜索,可以理解为交叉搜索,等价于坐标系;
3、前三种解法,维度越高,效率也就越高;
4、因为有“半小时”的时间约定,所以不能用简单的二分法来解答。所以,第四种解法用二进制为100瓶酒编码,进而用0和1对应不喝与喝(也对应了撞见毒酒后的生和死)。
5、那么第四种用二进制的解法,是否可以理解为“7维”的解法?
第一种解法有1个维度,该维度上有100种可能。这其中的99种,每种可能都需要1个侍卫去通过喝酒“消除不确定性”;
第二种解法有2个维度,每个维度上有10种可能,每种可能都需要1个侍卫去通过喝酒“消除不确定性”,然后这两个维度的交叉点,就是毒酒的位置;
第四种解法有7个维度,每个维度上有两种可能,每两种可能,只需要1个侍卫去通过喝酒,就可以“消除不确定性”。于是,这七个维度的交叉点(表述为一串二进制数字),就是毒酒的位置。
在这道题目中,使用二进制编码的策略是核心。通过将100桶酒编码为7位二进制数,我们能够用最少的侍卫(7个)来解决问题。
这种方法背后的原因是二进制的指数效应:每增加一位二进制位,就可以表示更多的状态,极大地减少了解决问题所需的资源(在这个例子中是侍卫的数量)。
相比于简单的线性搜索,二进制让我们进入了一个更高效的“维度”空间。
在这个空间里,每个侍卫只需要判断一个“0”或“1”的状态,就能为100桶酒中的每一桶赋予唯一的二进制编码。
这种策略不仅有效地消除了不确定性,还展示了通过增加维度解决问题的力量。
这一过程展现了升维和降维的相互配合:
升维思考:通过引入多个侍卫,每个侍卫相当于引入了一个新的维度,让我们能够从更多角度捕捉信息。
降维行动:通过侍卫生死的二值化状态,我们将所有复杂性压缩为一串二进制信息,这一信息指向毒酒的唯一桶号。
二
在上面递进的解体过程中,将二进制的方法,类比为7维,是一个有趣的想法。
进而,我们可以用一种更直观的方式,来阐述“升维思考、降维行动”。
我喜欢用可感知的思考来理解一些概念,而不是单靠文字本身的解释。
让我们再来看一道有趣的题目,以感知“维度”。
• 有三盏白炽灯泡和三个开关,每个开关控制一盏灯泡,但你不知道哪个开关对应哪个灯泡。
• 你可以进入一个房间控制开关,但灯泡在另一个房间,你只能进入灯泡房间一次来检查结果。
• 如何在最短时间内确定每个开关对应的灯泡?
聪明如你,即使知道答案,也不妨从维度的角度重新思考一遍。
难题在于,开和关只有两个维度,要想界定出三个灯泡,必须创造出一个新的维度。
白炽灯的另外一个属性是发热,所以可以引入“冷热的维度”。
这三种状态相当于在这个系统中添加了不同的维度:
• 亮/不亮的维度:开关是否正在控制灯泡。
• 热/不热的维度:灯泡是否曾被打开过但关闭。
• 冷/热的维度:灯泡的物理状态(热与冷)提供了额外的信息。
上面的冷和热,也是与时间的维度关联的。
事实上,精确而言,如上方法应该能够识别出四个灯泡。你觉得呢?
三
用类比和隐喻的方式,来表达一些主题,有“生动性”的优点,也有不精确的缺点。
再次声明,请你务必仅仅将其视为理解和感知的脚手架。
让我们回到数学和物理。
1854年,黎曼在哥廷根大学发表的演讲改变了数学和物理学的进程。他引入了一个革命性的概念:高维几何学,推翻了欧几里得几何的传统观念。
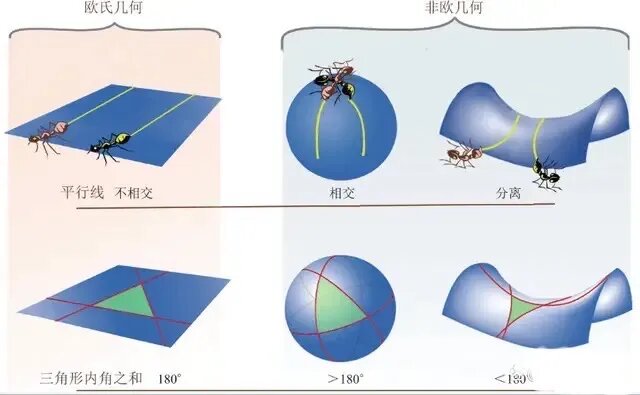
(图片来自网络)
在欧几里得几何中,空间是平坦的,二维或三维的,而黎曼发现了空间的弯曲性质,提出可以通过引入更高维度来解释自然界的现象。
黎曼的几何学不仅改变了数学的基础,也为物理学提供了新的工具。
尤其是在1915年,爱因斯坦借助黎曼的几何学,提出了广义相对论,用四维时空的弯曲来解释引力。黎曼的思想启发了后来的科学家,使他们进一步探索更高维的宇宙。
欧几里得几何学认为两点之间的最短距离是直线,而黎曼指出,这个定律只适用于平坦空间。
在弯曲空间中,比如球面上,两点之间的最短路径是曲线。黎曼通过引入“度规张量”这一工具,能够精确描述空间在每一点的弯曲程度。
这一创新让科学家可以用数学来描述任何维度的空间,无论是平坦的还是弯曲的。
更令人惊叹的是,黎曼的理论揭示了“力”可能只是空间几何变形的结果。
比如,当我们在三维空间中感受到引力时,实际上是因为空间在我们感知不到的第四维中发生了褶皱。这一概念为将来用高维几何学统一所有物理定律铺平了道路。
高斯较早前已经提出了平面“书虫”的思想实验,黎曼进一步将其扩充:
如果一张纸上生活着二维生物,把它们生活的纸褶皱之后,它们依然会觉得世界是平的,但当它们在褶皱的纸上运动时,它们就会感到一股看不见的“力”阻止它们沿直线运动。
黎曼几何不仅让爱因斯坦能够理解引力的本质,还让他开始思考,其他的自然力是否也是时空在更高维度中的褶皱结果。
这种思维方式为后来物理学家尝试统一电磁力、弱力和强力奠定了理论基础,并成为现代超弦理论的先声。
黎曼还提出了“黎曼切口”的假设,在这一模型中,两张纸代表两个不同的二维曲面,切口则是这两个曲面之间的通道。
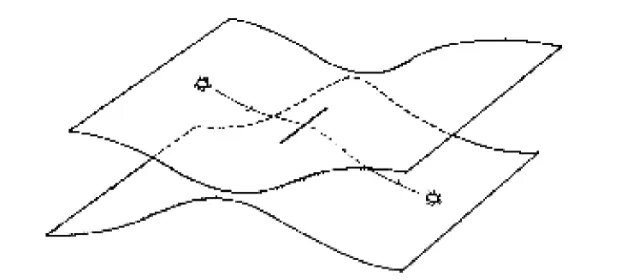


保持联系
北京市朝阳区东三环中路63号楼富力中心1612室
邮编:100022
电话:010 5903 7060
传真:010 5903 7060
上海市普陀区西康路1143号鸿寿坊东塔2108室
邮编:200060
电话:021 6333 3765
传真:021 6333 8821
湖北省武汉市硚口区恒隆广场办公楼3804室
邮编:430030
电话:027 8771 8808
浙江省杭州市钱江世纪城润奥商务中心T2写字楼1712室
邮编:310012
深圳市南山区深南大道9676号大冲商务中心C座2709室
邮编:518000
海南省海口市秀英区兴国路10号海南人才大厦3层A319-2 室
邮编:570100