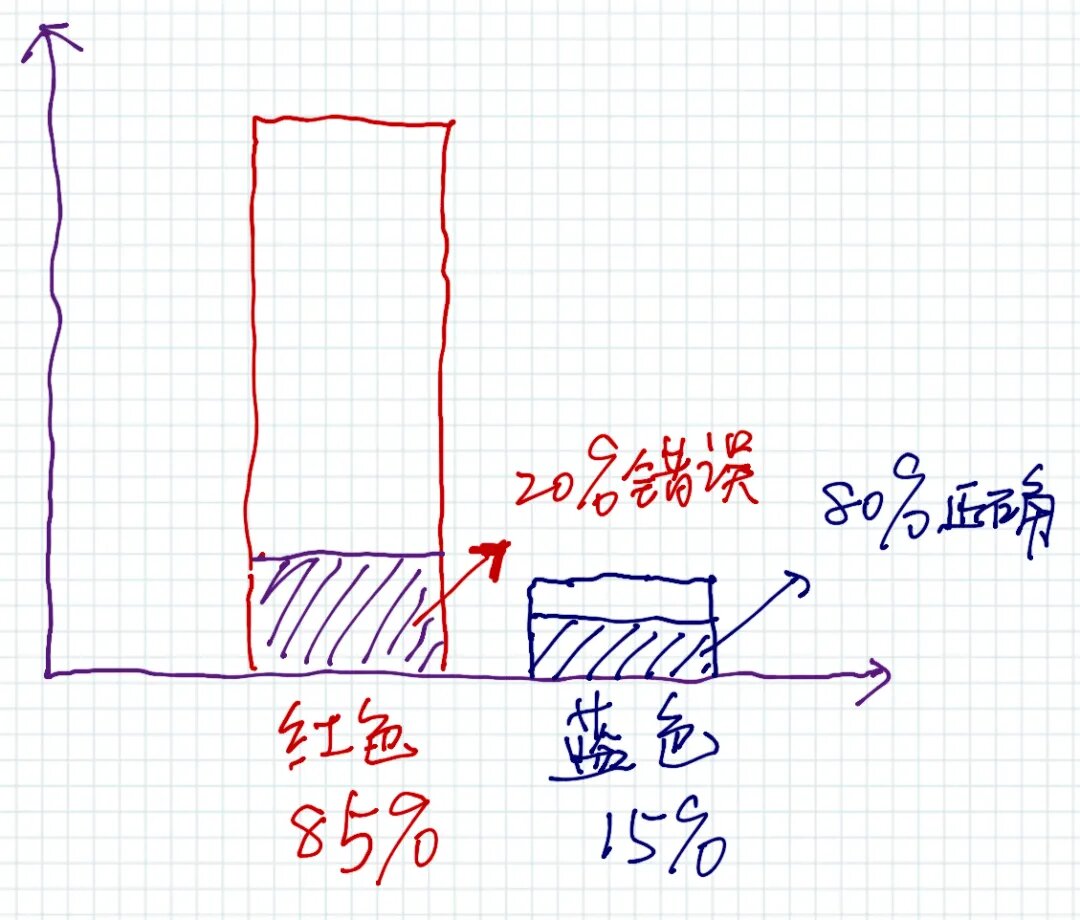
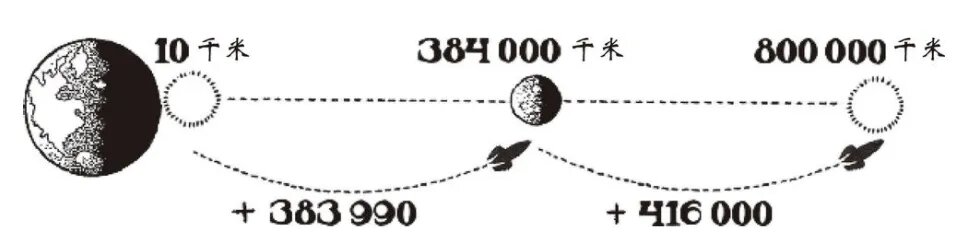
下图是对公式的直观描述：

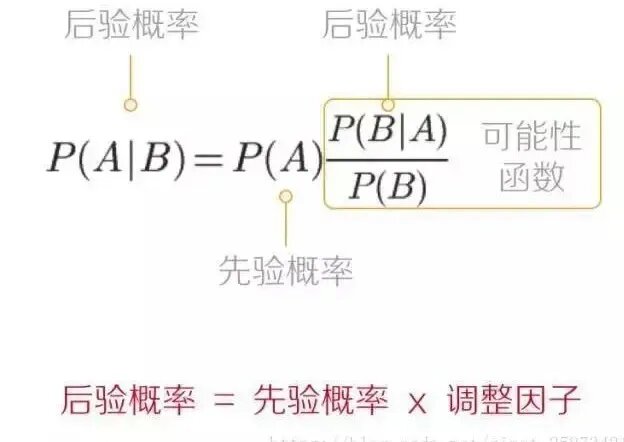
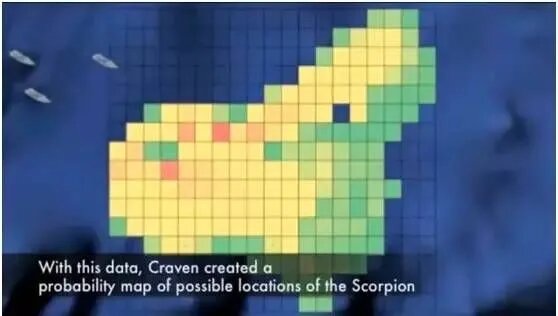
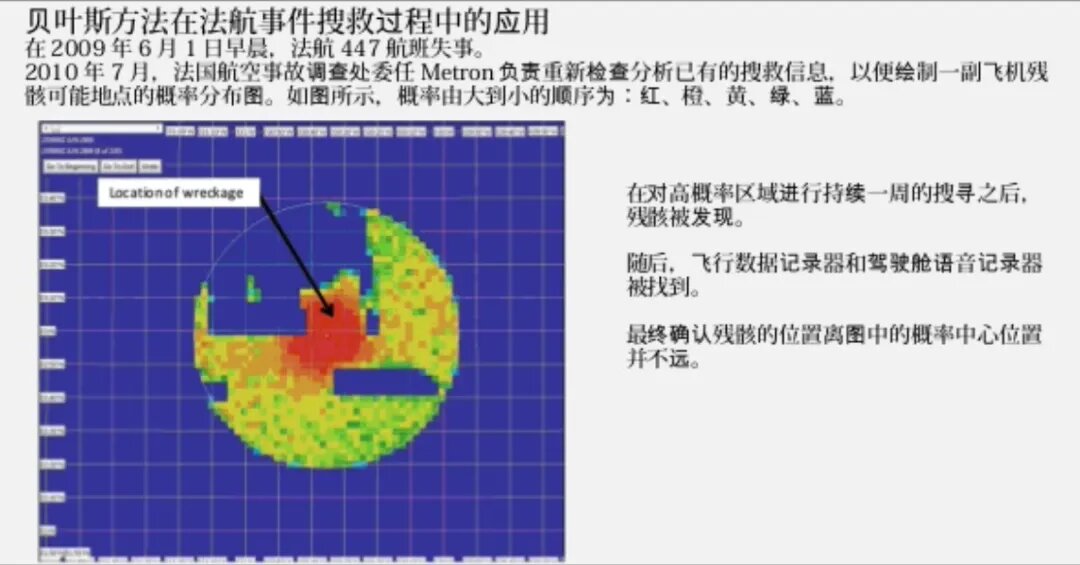
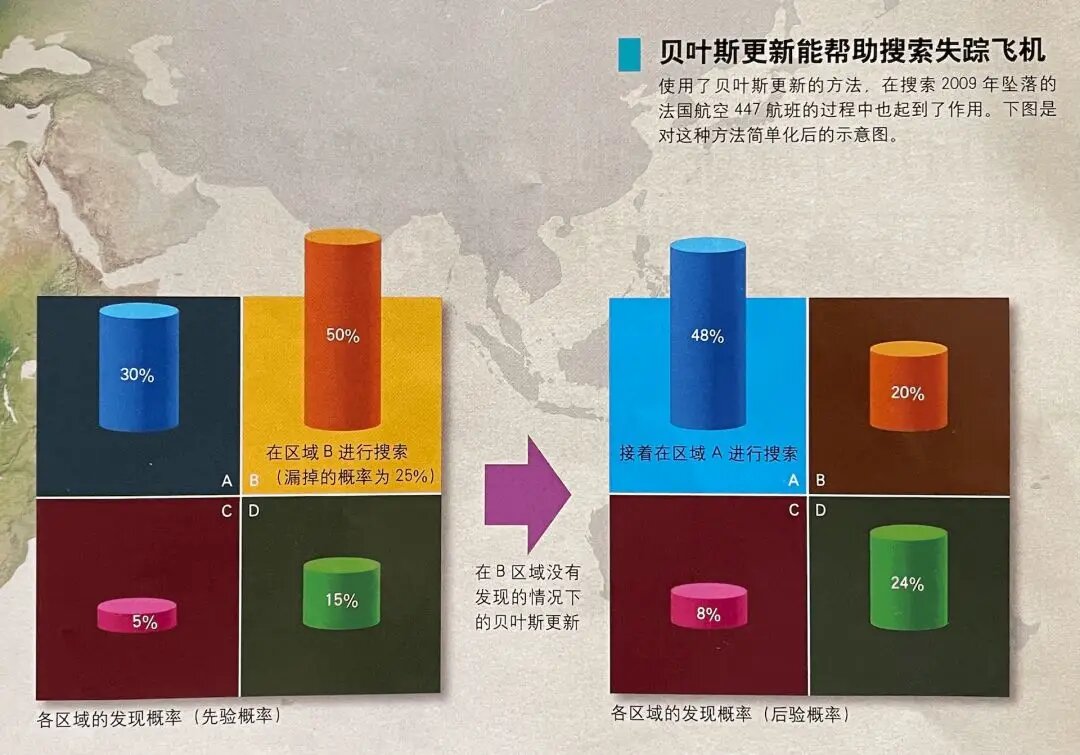
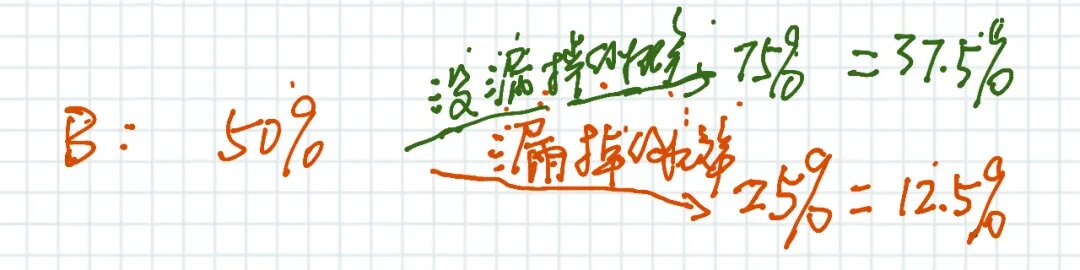
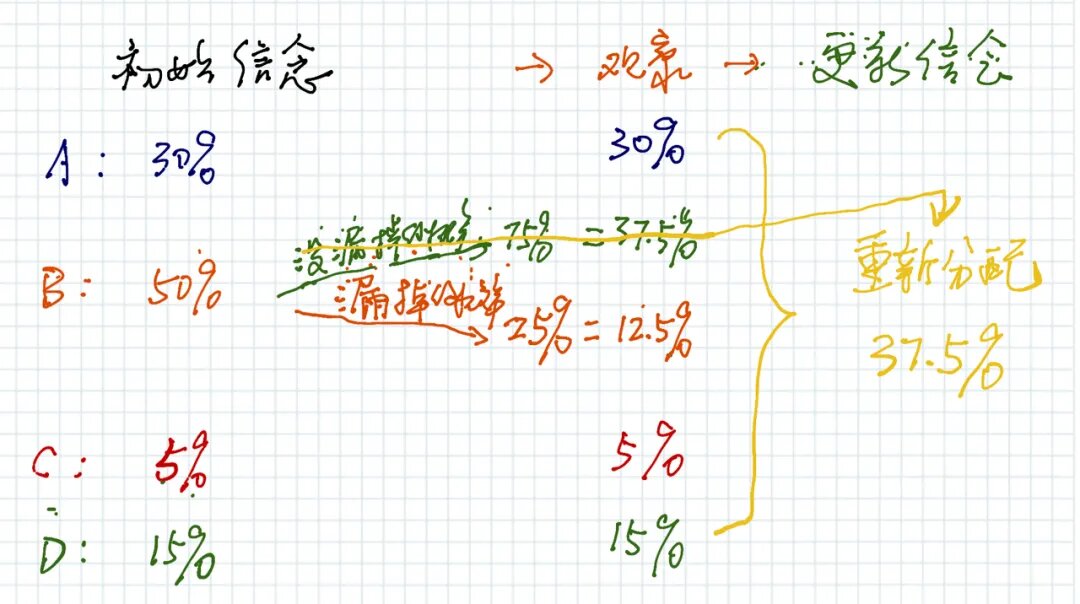
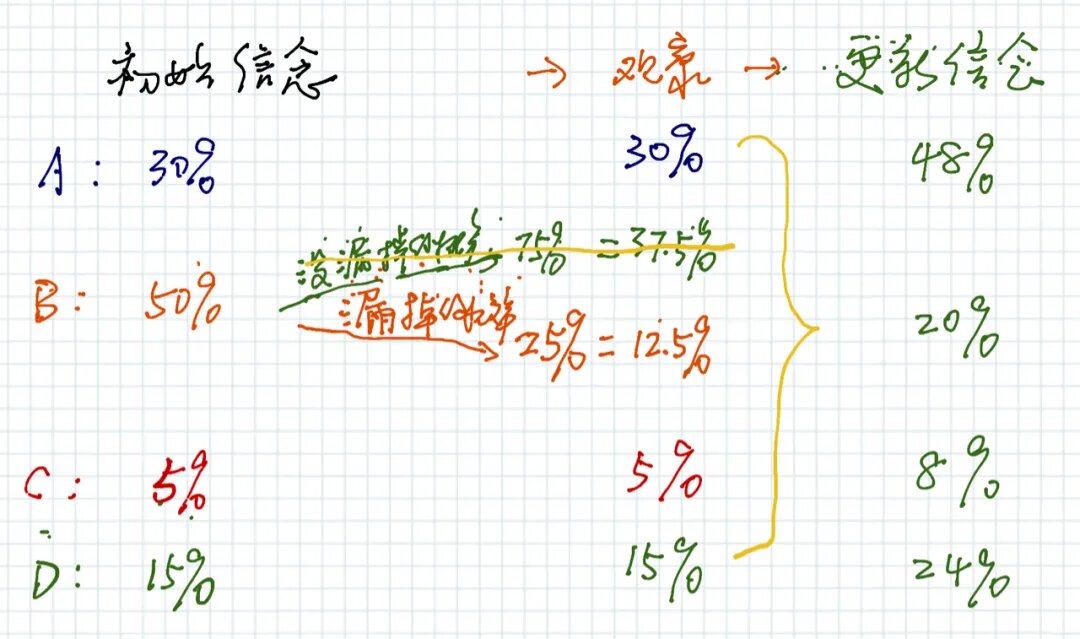
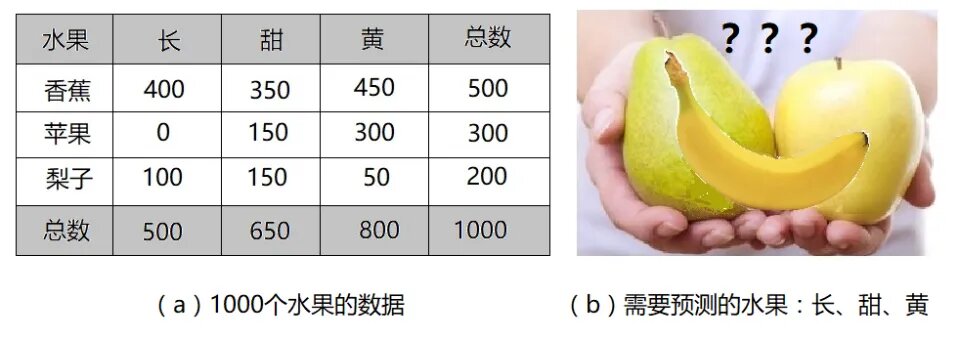
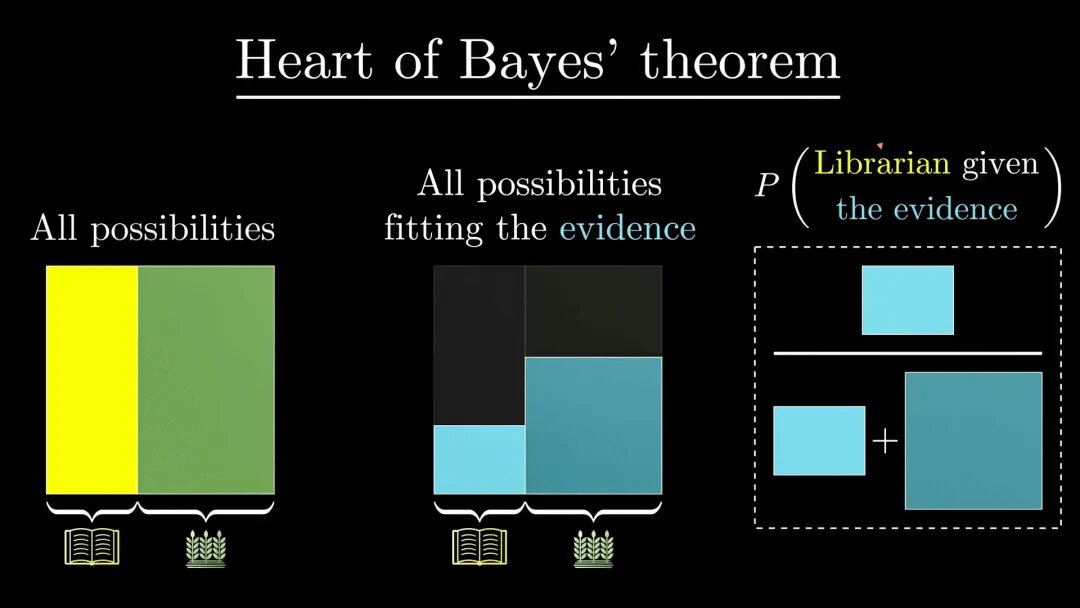
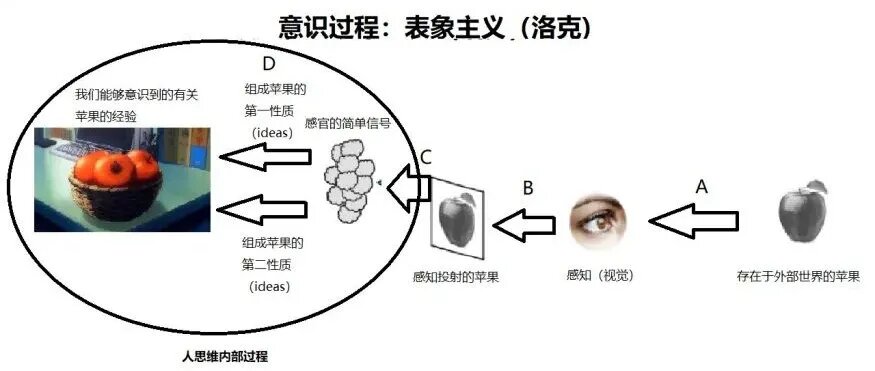
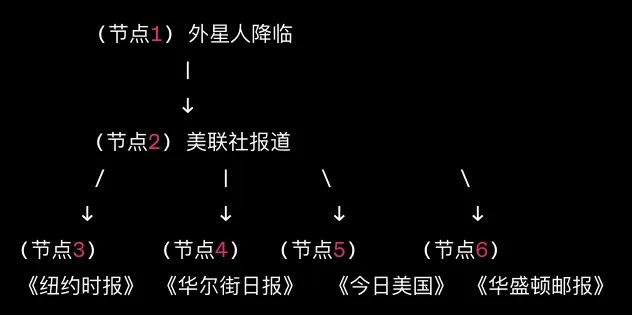
贝叶斯网络是一种用于表示变量之间条件依赖关系的概率图模型。它通过有向无环图来表示这些关系。

在上图中，节点代表随机变量（它们可以是可观察到的量、未知参数或假设等），而有向边则表示一个变量可能如何影响另一个变量。

20世纪70年代末，人工智能领域针对如何处理不确定性因素展开了激烈讨论，各种主张层出不穷。

在1982年，“贝叶斯网络”之父朱迪亚·珀尔提出了一个表面上平淡无奇但实际上非常激进的建议：

将概率视作常识的“守护者”，聚焦于修复其在计算方面的缺陷，而不是从头开始创造一个新的不确定性理论。

更具体地说，我们不能再像以前那样用一张巨大的表格来表示概率，而是要用一个松散耦合的变量网络来表示概率。

贝叶斯网络有如下特点：

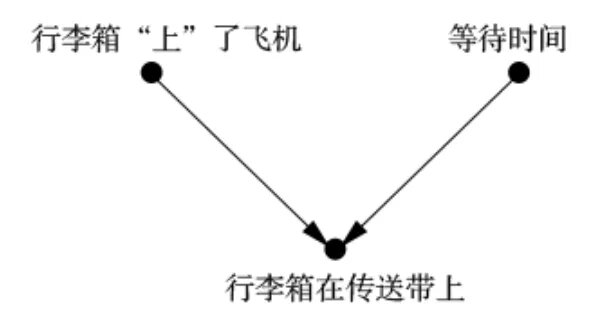
1、条件依赖性：贝叶斯网络通过图的形式表达了条件依赖关系。如果一个箭头从A指向B，那么B在一定程度上取决于A。

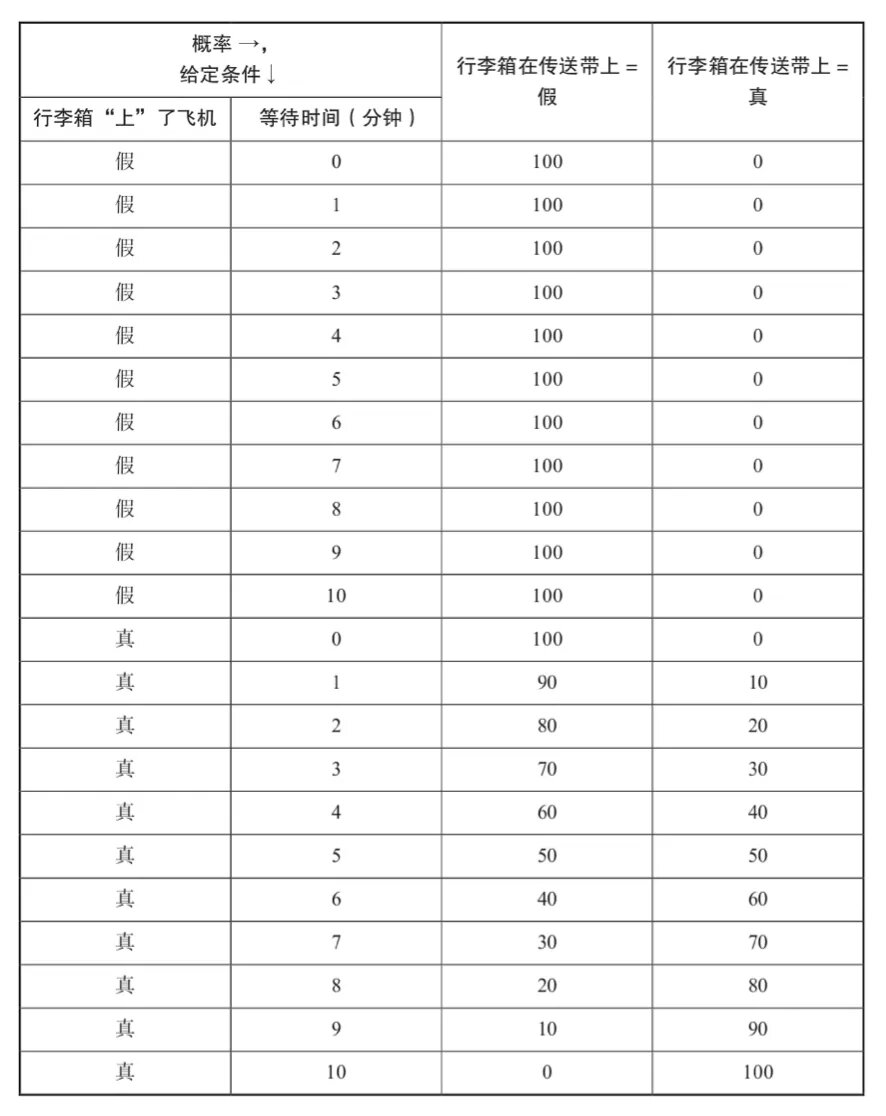
2、概率性：每一个节点都有一个条件概率表，用于描述给定其父节点状态下该节点状态的概率。

3、推理与学习：给定一部分节点（观测数据），你可以使用贝叶斯推断来估算其他未观测节点（隐藏变量）的概率分布。

贝叶斯网络的强大之处在于，即使在复杂和不确定的情况下，它也能提供一种逻辑严谨的方式来推断未知变量的概率分布。

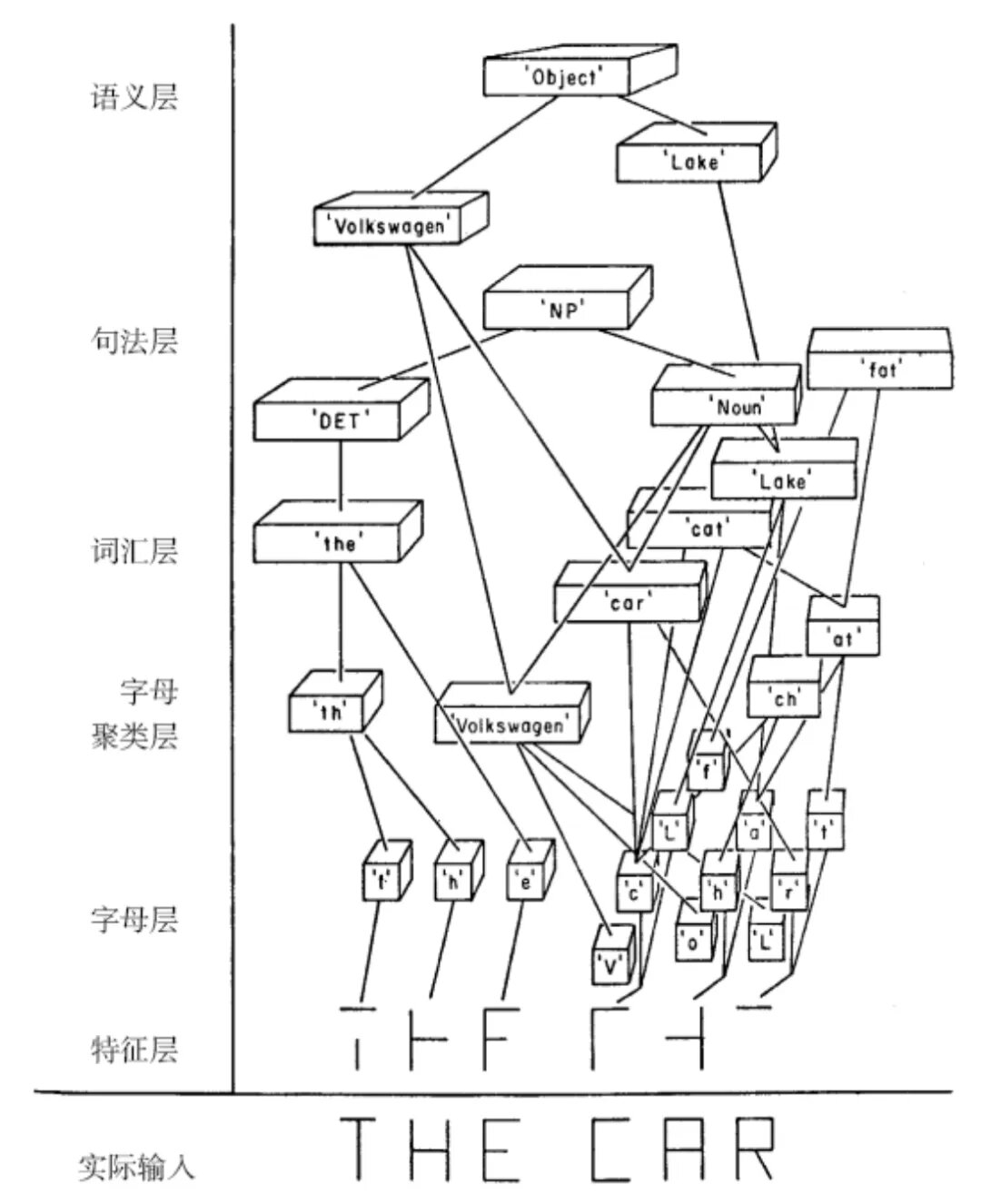
1、在字母层面上，它可能是“FHP”，但在词汇层面，这个字母串是没有意义的。

2、在词汇层面上，这个词更可能是“FAR”、“CAR”或“FAT”。神经元将这些信息向上传递到句法层面，我们因此判断出在“THE”之后出现的应该是一个名词。

3、最后，这些信息被传递到语义层面，我们进而意识到因为前一句提到了大众汽车，所以这个短语很可能是“THE CAR”，代指同一辆大众汽车。

更关键的是，从上图中我们可以发现：

“所有的神经元都是同时来回传递信息的，自上而下，自下而上，自左向右，自右向左。”

这意味着，大脑是一个高度并行的系统，而非过去我们认为的是一个单一的、集中控制的系统。

朱迪亚·珀尔从鲁梅哈特的论文中认识到：

任何人工智能都必须建立在模拟我们所知道的人类神经信息处理过程的基础上，并且不确定性下的机器推理必须借助类似的信息传递的体系结构来构建。

然而，难题是：信息具体指的是什么呢？

想了好几个月，朱迪亚·珀尔终于认识到：

信息是一个方向上的条件概率和另一个方向上的似然比。

更进一步，他将贝叶斯定律和神经网络的推理结合了起来。

朱迪亚·珀尔认为：

1、网络应该是分层的，箭头从更高层级的神经元指向较低层级的神经元，或者从“父节点”指向“子节点”。

2、每个节点都会向其所有的相邻节点（包括层次结构中的上级节点和下级节点）发送信息，告知当前它对所跟踪变量的信念度（例如，“我有2/3的把握认为这个字母是R”）。

3、接收信息的节点会根据信息传递的方向，以两种不同的方式处理信息。

4、如果信息是从父节点传递到子节点的，则子节点将使用条件概率更新它的信念。

贝叶斯网络中的每个节点（变量）通常只与其父节点和子节点有直接的依赖关系，这大大减少了需要考虑的变量数量和相应的计算负担。

故事的另外一条主线，顺着神经网络前行。

1986年10月，大卫·鲁梅尔哈特、杰弗里·辛顿和罗纳德·威廉姆斯发表了《”Learning representations by back-propagating errors》。

该论文描述了一种新的学习程序，可用于神经元样网络单位的反向传播，其掀起的惊人浪潮，正是当下大热的深度学习。‍‍‍‍

必须一提的是，朱迪亚·珀尔试图将因果引入概率世界。而在神经网络原教旨主义者辛顿看来，许多类似的主张完全是多余的。

*文章为作者独立观点，不代表朴谷咨询立场。