

发布时间:2021-06-11 17:00
作者:admin
编者荐语:
有一把刀,你应该时常握在手里面。
今天我们就来看一下这把刀是如何帮你看清这纷繁混乱的世界。
以下文章来源于量子学派 ,作者白格尔&冯诺
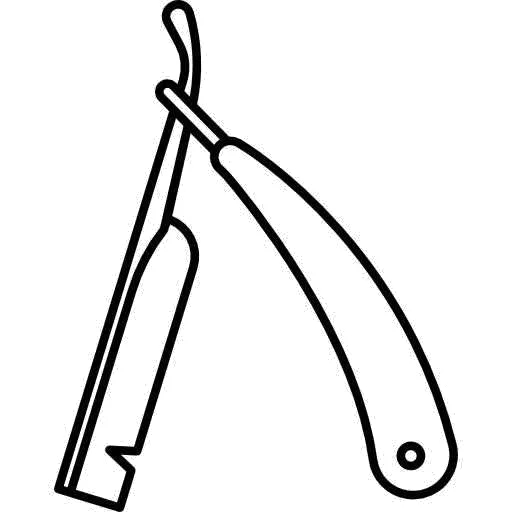
——这柄真相之刃,让人类看清真相

人类曾经拥有一把刀;
它重量不如匕首,锋利胜过屠龙;
它貌似轻如鸿毛,出手横扫千均。
它纵横于哲学、物理、经济、语言学、管理学等领域;
迷惑了哲学家,激励了科学家,引领着企业家;
自14世纪横空出世后,它终结了繁琐复杂的学院争论;斩杀了卡尔·萨根的恐怖火龙。

它就是那把小小剃刀,名字叫做奥卡姆。
奥卡姆剃刀
14世纪时,欧洲学者忙于“口遁”,把研究“似是而非”的东西当作智慧象征。
例如:
黑色的白伞是否存在?
上帝的喷嚏还是哈欠导致了电闪雷鸣?
不是张三、也不是李四的人本身是否存在?
这些问题与中国的“白马非马,楚人非人”的诡辩学说,与“不是风动也不是幡动而是心动”此类无法证伪的观点有异曲同工之妙。
来自英格兰奥卡姆的逻辑学家威廉对此极其厌烦,这些学者争来争去全无实据,那口沫横飞的星子时常喷到威廉的脸上。
如果不是作为一个有教养的修士,他会直接说“你丫闭嘴”,最后他压制住满腔怒火,文诌诌地道:如无必要,勿增实体。

非常简单八个字,道出了事物本质。
通俗一点的解释:
如果能用A来描述现象,那么不要发明B来解释,新逻辑可能有漏洞。
延伸一点的理论:
如果同一个现象有n种理论,最简单的那个便是最正确的。
他再进一步提出一条实践原理:
能用n做好事情,那就不要有第n+1个动作。
这一把小小的剃刀,貌似简单,它却在不同学科中展现出巨大威力。
逻辑学应用:
斩杀“喷火的龙”
首先它斩杀了卡尔·萨根车库里的那条喷火的巨龙,让逻辑回归到正常状态。
“我的车库里有一条喷火的巨龙。”卡尔·萨根说。
卡尔的朋友问:“在哪里,我看看。”
“这条龙是隐形的,是看不见的。”卡尔·萨根故作高深。
“那真可惜,”朋友道,“让我摸摸它的逆鳞。”
“隐形的龙,不是想摸就能摸到的。”
朋友想了一下,“让它来喷我吧,我愿意测测火焰温度。”
“这条龙喷出的火是没有温度的,那是无形的温度。”
“那在地上撒上石灰,记录下龙的抓印。”
“这条龙是浮在空中的,不会在地上留下印痕。”卡尔又道。
“那,”朋友犹豫了一下,“总归有一种方法才观察到这条龙吧?”
卡尔·萨根道:“不,你提出任何一种观察方法,龙都有相应特性来避免观察。”
那么问题就来了,一条看不见摸不着,喷着没有热量的火,浮在空中不会留下足迹,用任何一种方法都观察不到的龙,同根本就没有龙,有什么区别呢?
这就是奥卡姆剃刀的标准应用:卡尔·萨根是个骗子,他的车库里根本就没有龙。
科学应用:
最小作用量原理
宇宙所有的规律,都要服从一些基本原理,如简单、对称、守恒、稳定。
还有一个很重要的原理:最小作用量原理(principle of least action)。
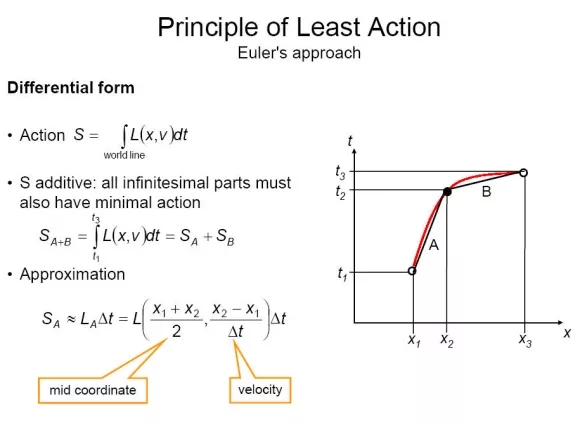
作用量S是拉格朗日函数的时间积分,含义很广,包括时间、空间、能量、概率。
作用量最小,意味着数学上的极小值、导数为零。
自由落体为什么会沿直线下落?光为什么沿直线传播?因为在近似平直的三维时空中,直线运动消耗的空间和时间作用量最小;在非平直的时空中,如球面,物体会沿着最短圆弧(测地线)运动;无重力环境下,物体会收缩成球形,因为体积不变时,收缩成球面积最小。
狗叼飞盘,走的是直线,因为时空消耗最短;而狼捕捉猎物,走的是弯曲路线,它要的是捕获概率最大(失败率最小),概率超过时空成为第一作用量。

亚里士多德说,自然选择最短道路。事物按照最小作用量运动,是为了尽量减少自己的消耗。因此,它们用数学最优化方式维持自己的“生命”,延迟衰亡。

生物学应用:
进化论的耗能最小原理
生物除了适应性这个原则之外,还要厉行节约能量、体积、器官数量。
北方生物的特点,都是为了减少单位表皮上的散热。因为北方比南方寒冷,谁能更好地保温,谁就能在北方存活。

(表面积与三维生物的半径平方正比,体积与半径立方正比。表面积与体积之比越小,散热越慢。)
蟑螂能够扩散到全球,是因为它们占据了一种特殊的生态位:不挑食,什么都吃;不挑环境,什么样的肮脏环境都接受;体型很小,不仅吃得少,还易于被携带和躲藏;动物中常见的勇猛和骄傲对它们来说是成本很高的累赘。

蟑螂把生存成本压缩到极低程度,以至于没有生物在这个生态位上和它竞争,成为世界上最适应环境的甲壳动物。
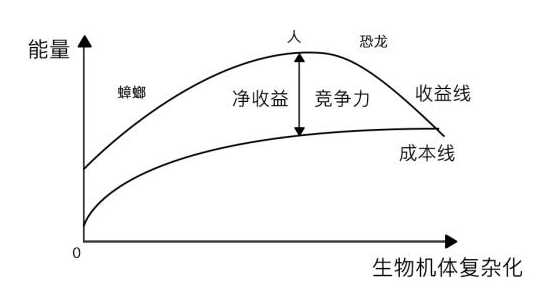
节约能量和扩大收益之间的关系是动态的,最重要的是两者之间的差额。新增器官可能消耗更大能量,但也能带来更大收益;同样的收益,你能节约能量,你就获得生存优势。
大自然不做无用功,进化论亦如是。
经济学应用:
税收中的“拉弗曲线”
在经济系统中,税收是关键性控制手段之一。
那到底该如何调整税收呢,这是执政官们最烦恼的问题。
当年司马光和王安石在这个问题争执了一辈子,好友最终成为仇敌。
假设植物学家A和B争论西红柿是水果还是蔬菜,如果是水果则面临高税,而蔬菜由于是基本消费品则征低税或不征税。僵持不下,决策者C如何选择?
答案是,既然西红柿的生物学身份争议不清,那么就按照法律管制是必要的恶的原则,把西红柿当成蔬菜不征税。因为征收行为本身需要人力物力,很可能消耗的资源会超过征收带来的好处。
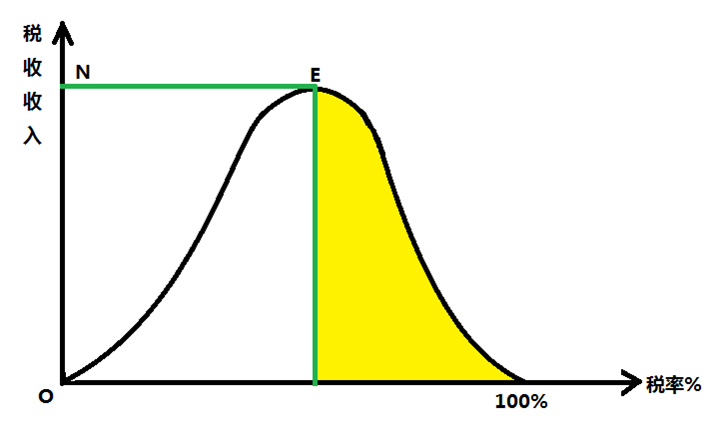
拉弗曲线:E点表示税收最高点;黄色区域为禁止收税区
美国供给学派经济学家拉弗在1974年提出这个简单的税收曲线模型:
税收一旦超过最优点,税收就会抑制个体和企业的活力,导致政府税收下降,不仅如此,还会导致整个社会的活力受损。
拉弗税收曲线的含义就是:如无必要,切勿加税。
语言学应用:辞简义赅
热门古装电视剧《清平乐》里谈到一个史诗级典故,讲的是大文豪欧阳修的轶事。
剧本来源于冯梦龙的《古今谭概》,原故事如下:
当年欧阳修在翰林院任职时,一次,与同院三个下属出游,见路旁有匹飞驰的马踩死了一只狗。
欧阳修提议:“请你们分别来记叙一下此事。”
一人率先说道“有黄犬卧于道,马惊,奔逸而来,蹄而死之”。
另一人接着说:“有黄犬卧于通衢,逸马蹄而杀之。”
最后第三人说:“有犬卧于通衢,卧犬遭之而毙。”
欧阳修听后笑道:“像你们这样修史,一万卷也写不完。”
那三人于是连忙请教:“那你如何说呢?”
欧阳修道:“‘逸马杀犬于道’,六字足矣!”
三人听后争相点赞,比照冗赘,深为欧阳修为文简洁折服。
语言学应用的极高境界,就是言词简洁、辞简义赅。
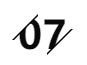
数学应用:极简方式解决
网上有举到一个数学方面的例子:
一串数列:-1,3,7,11, ( ),( ),
括号中应该填什么呢?
答案1:15,19,因为这是一个首项为-1,
公差为4的等差数列;
答案2:-19.9.1043.8,它满足一个
-x^3/11+9/11x^2+23/11的多项式数列。
很明显答案1就比答案2有说服力,越做出无必要的复杂化说服力越弱。
《从一到无穷大》里面有一个“寻找藏宝”的例子,也展示数学的极简化能力:
有个年轻人在遗物中发现了一张宝藏图。图上这样写着:乘船至北纬X度 、西经Y度,能看到一小岛,岛上草地上有一株橡树和一株松树,还有一座绞架。
从绞架走到橡树,并记住走了多少步;到了橡树向右拐直角再走这么多步,在这里打个桩。然后回到绞架那里,朝松树走去,同时记住所走的步数;到了松树向左拐个直角再走这么多步。
在这里也钉个桩。在两个桩的正当中挖掘,就可找到宝藏。
这道指示很清楚、明白。所以,年轻人开心到不行,然而当他找到这座岛时大失所望,因为参考点绞架不见了。

这个时候如果抛弃掉那些复杂文字表述,只要列出一个复数坐标函数:
Γ=a + bi
很快就可以计算出,Γ所表示的未知绞架的位置已在运算过程中消失了。不管这绞架在何处,宝藏都在+i这个点上。
绞架的位置那个信息其实是冗余的,这位年轻人无须在整个岛上挖来挖去,他只要在图中打×处一挖,就可以把宝贝弄到手。
社会学应用:
看清真相,远离骗局
奥卡姆剃刀在社会学上有更多应用,例如:
信息爆炸时代,大部分信息没有价值,完全可剔除掉。
商业物欲时代,各种渠道提示买买买,可实际上,最美好的生活是扔东西。
在服饰设计层面,最好的设计就是用最简洁的方式利用好整块布。
在企业管理当中,复杂的组织架构非但不能提升效率,反而导致信息不畅。
知识付费时代,鸡汤内容不能使让人见识增长,反而会增加知识焦虑。
很多时候,留白比什么都重要。
除了以上这些,奥卡姆剃刀最重要的应用是洞察真相,看清骗局。
皇帝有没有穿衣服?
让我们来戳穿骗子的逻辑,《皇帝的新衣》的皇帝到底穿没穿衣服呢?
别以为这个问题好回答,如果你在现场,你很有可能就是大臣之一。

如果懂得了奥卡姆剃刀原理,可以用逻辑手段,判断谁是真理。
第一种逻辑如下:假设皇帝是真的穿了衣服→假设愚蠢的人看不见→假设你就是愚蠢的人→所以你没看见皇帝穿衣服。
第二种逻辑如下:假设皇帝没穿衣服→所以你没看见皇帝穿衣服。
同样看见光身子的皇帝,第二种解释简单明了。而第一种解释,可能正因为它是错误的,就需要更多假设来补救漏洞,就像说谎圆谎一样。
真相不需要伪装掩饰,简单明了。
金字塔式“庞氏骗局”?
庞氏骗局是对金融领域投资诈骗的称呼,是金字塔骗局始祖。
利用人性贪婪,这样的骗局比比皆是。庞氏骗局在中国又称“拆东墙补西墙”、“空手套白狼”。
里面的套路非常多,各种表述也特别复杂,一般人都会看得眼花缭乱。

如果你是第一次去上课,碰上一个口才不错的骗子,一定会热血沸腾,感觉自己躲在床上就可以日进斗金。
但如果你懂得奥卡姆剃刀原理,只要问一句:那这个系统到底谁来买单,财富谁来创造?不可能全部都是赢家。
这个时候你就会明白:原来自己就是传说中的韭菜。
迷信的逻辑源头不可证伪
举一个例子:你坐在庙里,一阵风把庙门吹开了。
正常逻辑:外面风太大,门被空气顶开。
迷信逻辑:你心不诚,神鬼发怒,神鬼驱使空气流动,门被空气顶开,所以你心要诚。
可见迷信逻辑比正常逻辑要复杂,很多人利用这一点装神弄鬼。
还有那些神心灵、波仁切的骗局,都夹杂了许多伪逻辑在里面。
根据奥卡姆剃刀,迷信逻辑解释比正常逻辑弱得多。
心不诚不可证伪,神鬼亦不可证伪。
神药的逻辑为什么复杂
市场上总是流传着一些神药,在中老人里面尤其有市场。
这些药是如何推销的,我们看看他们的传销逻辑。
第一:这个药有非常好的辅助治疗作用;
第二:我们的药都符合国家相关规定;
第三:电视台都有我们的广告;
第四:某某名人也喝过我们的营养液;
第五:某某吃这个治好了多年的中风;
…………
它有非常多的逻辑,有的甚至把周易、阴阳八卦、五行风水搅和在一起,你根本就看不清楚它的逻辑线在哪里。
其实很简单,亮出你的奥卡姆剃刀:这个药为什么有效,有效药理是什么?
…………

社会上的骗局还有非常多,如果一件事情它变得非常复杂,还夹杂了许多新概念,这种项目最值得人怀疑。
如果逻辑完整自洽,越简洁的解释越有力。
比奥卡姆还要厉害的剃刀
我说了这么多,同时也在违背奥卡姆剃刀理论。
奥卡姆剃刀讲的是简单即效率,但为何还要借助迂回比喻?
剃刀情急之下可以用来论证哲学命题,但这终究不是剃刀使命。

这把刀,你应该时常握在手里面。
因为它是真相之刃,帮你理清这“剪不断,理还乱”的世界。
手持这把刀的人,既清醒,又智慧。
可惜的是,人类大多数已经迷失,在这复杂的世界、荒谬的骗局中忙乱奔走,慢慢地,已经忘记了这把最锋利的思想之刀。

当年,人类获得这把刀并不容易,剃刀主人威廉被视为异端,教会驱逐,帝国流放;死后经过笛卡儿、牛顿等大科哲加持后,历经百年,才磨成这闪闪发亮的理性刀片。
倘若这位14世纪的修士知道他的武器被人类遗忘,除了感慨一生流离外,会更加绝望于这个世界。
记住,这是真相之刃,锋利无敌。
有骗局袭来时,拿起这把刀。
它是骗子最害怕的武器。
世界越来越复杂时,也祭起这把刀。
看清楚世界的真相。
“本文转自公众号 量子学派——专注于自然科学领域(数理哲)的教育平台”
┌
朴谷咨询(PGA)是一家聚焦于互联网、高科技、消费、教育、文娱与医疗行业,提供投融资及并购交易顾问、尽职调查、财务与税务咨询服务的专业机构。
朴谷已累计服务超过500个投融资与并购交易案例。我们的专业人员拥有丰富的行业经验,为投资机构与企业客户提供最具深度与增值的专业化服务。
┘

保持联系
北京市朝阳区东三环中路63号楼富力中心1612室
邮编:100022
电话:010 5903 7060
传真:010 5903 7060
上海市普陀区西康路1143号鸿寿坊东塔2108室
邮编:200060
电话:021 6333 3765
传真:021 6333 8821
湖北省武汉市硚口区恒隆广场办公楼3804室
邮编:430030
电话:027 8771 8808
浙江省杭州市钱江世纪城润奥商务中心T2写字楼1712室
邮编:310012
深圳市南山区深南大道9676号大冲商务中心C座2709室
邮编:518000
海南省海口市秀英区兴国路10号海南人才大厦3层A319-2 室
邮编:570100